Mar. 19th
Tuesday
2013 AD
【行星大戰】
前言
《行星大戰》是大外星人伊琉沙於地球紀元2010年開發的一門天文科普課程,其內容相較於理論天文物理要簡單許多,課程內容將從人類自古對於行星的理解延伸至今日地球人對於行星的定義,隨著日月星辰流轉,多少個春秋,我們對於行星的認知一直在改變,也造成了歷史上兩次對於行星理解上有重要突破,伊琉沙將其稱之為「行星大戰」,而是否未來又有另一波行星大戰,其實仍舊有更多的未知數。
課程章節:
- 行星大戰概述
- 七曜
- 中國行星觀測史
- 遊走者
- 多重行星體系的對話
- 行星的和諧
- 新星崛起
- 行星新勢力
- 行星大戰
- 進擊的小行星
- 筆尖下的行星
- 行星門
- 祝融星
- X行星
- 第九大行星
- 行星新視界
- 第十大行星?
- 行星大戰再起
- 雙行星與草案
- 行星定義決案
- 冥王星的歸宿
- 矮行星及候選者
- 縱觀太陽系天體
- 天體命名規則
- 系外行星適居帶
- 克卜勒任務
- 超級地球大戰
- 神秘低哇咔咔星系
- 星際大戰與死星
- Bonus
行星大戰概述
行星大戰之名的靈感來自於21世紀初,木星與土星發現的衛星數量激增,有人以衛星大戰稱之,而伊琉沙在經歷太陽系從九大行星變成八大行星的整個歷程中,深入了解冥王星在這次事件中所扮演的角色,偶然有偶地是,在一百五十年前的十九世紀上半葉,天文學界也曾重新思考過怎樣才算是一顆行星,而迫使天文學家重視這個問題的導因皆是在太陽系發現的新天體,這與衛星大戰的形式如出一轍,故咱將這個天文學史上重大的事件稱作行星大戰,而這個課程將從古老東西方對於行星的認識開始說起,而至今日太陽系天體的分門別類,更將行星問題推廣至系外行星,追根究底,定義正是人類所制定的,所以問題的源頭勢必就是人類認知上的差異。
七曜
 從上古中國說起,中國對於日月星辰的了解可追溯遠古弇兹氏(距今約三萬多年),而究竟確切何時其實並不明確,但人們對於自然界七顆明亮的天體已有一定程度的觀測,這七顆被稱作七曜,是作為對日月五星的總稱,也稱作七緯或七政,在典籍中,七政一詞有詳盡的解釋。
從上古中國說起,中國對於日月星辰的了解可追溯遠古弇兹氏(距今約三萬多年),而究竟確切何時其實並不明確,但人們對於自然界七顆明亮的天體已有一定程度的觀測,這七顆被稱作七曜,是作為對日月五星的總稱,也稱作七緯或七政,在典籍中,七政一詞有詳盡的解釋。
《尚書.舜典》:「:在璿璣玉衡,以齊七政。」
漢.孔安國傳:「在,察也。璇,美玉。璣、衡,王者正天之器,可轉運者。七政,日月五星各異政。舜察天文,齊七政,審已當天心與否。」璿音璇。
唐.孔穎達疏:「在七政,其政有七,於璣衡察之,必在天者知七政,謂日月與五星也。木曰歲星,火曰熒惑星,土曰鎮星,金曰太白星,水曰辰星。」
而七緯一詞則係古人以天為左旋,是為經,日月五星右旋,則為緯,因此得七緯之名,若此五星則稱五緯,是為緯星,而列天左旋之星,則稱作經星或列星,因其排列在天有常,意即今日之恆星。
《周禮.春官宗伯第三》:「以禋祀祀昊天上帝。以實柴祀日月星辰。」
漢.鄭玄注:「星謂五緯,辰謂日月所會十二次。」
唐.賈公彥疏:「星謂五緯者,五緯即五星。東方歲星,南方熒惑,西方大白,北方辰星,中央鎮星。言緯者,二十八宿隨天左轉為經,五星右旋為緯。」
《史記.天官書》:「余觀史記,考行事,百年之中,五星無出而不反逆行,反逆行,嘗盛大而變色;日月薄蝕,行南北有時:此其大度也。故紫宮、房心、權衡、咸池、虛危列宿部星,此天之五官坐位也,為經,不移徙,大小有差,闊狹有常。水、火、金、木、填星,此五星者,天之五佐,為緯,見伏有時,所過行贏縮有度。
唐.張守節《史記正義》:「『此五星者,天之五佐』,言水、火、金、木、土五星佐天行德也。」
對於七曜的描述自古既有,其明顯是較為晚期用作星期上的對應,即七曜日,這種紀日規則並非中國原有,而是唐朝時從印度傳入的《宿曜經》所引入,中國將其與二十八宿結合,而這種習慣於民國時改名為星期,但今日東亞的韓國與日本仍舊保留這樣的稱呼。
中國先人除了對日月已有廣泛的知識,也對五星觀測留有詳盡的資料,如戰國時代偉大的天文學家-甘德,其其中一部著作《歲星經》就是一部對於木星觀測的鉅作,可惜此書早已失傳,中國天文史學家席澤宗於1981年就推斷甘德可能在公元前346年就已發現了木衛三(Ganymede,Jupiter III)這顆太陽系最大的衛星,這可比義大利天文學家伽利略(Galileo Galilei)發現木星衛星要早將近兩千年,儘管今日學界普遍並不認可此一說法,但無可厚非地是對於行星有如此詳盡的觀測記錄,西方在當時是遠不及中國的,且伊琉沙深信甘德才是木衛的發現者,哇咔咔。
另一項證據是公元1973年在中國長沙發現的馬王堆漢墓,其中三號墓出土了大量的帛書,其中有八千餘字的記載被整理成《五星占》,其內容除了包含五星運行的記載占文外還附有《五星行度表》,最大的貢獻莫過於記載了金星、木星與土星三者的會合週期與恆星周期(恆星年),這樣的成就遠遠領先西方。
中國行星觀測史
暫無文字
遊走者
遊走者(Wander),作為今日行星詞源的前身形容地很貼切,西方文明起源於古美索不達米亞,其中在古巴比倫時代(距今約四千年,相當於華夏文明的上古時代)就已有豐富的天文數學知識,且當時已能區分行星與恆星,這些知識後來被古希臘人吸收,而Πλανήτης的稱呼就是這時候誕生的,其意思就是漫無目標的流浪者,類似的概念在1792年本木良永翻譯哥白尼的《地動日心說》中將其翻譯成惑星也有類似的意思。
古希臘天文學的發展成就在古風時期,古希臘人以希臘神話的人物為這些行星命名,後來羅馬人將其轉換成羅馬名字成為今日行星的英文名字;而Πλανήτης則被譯作為Wandering star,意即漫遊的星星,近代中文則將其翻譯成行星。
多重行星體系的對話
伊琉沙將本篇標題取名為多重行星體系的對話,是為了向小時候最崇拜的偉人-伽利略致敬,伽利略(Galileo Galilei)於公元1632年出版的鉅作《關於托勒密和哥白尼兩大世界體系的對話》(Dialogo sopra i due massimi systemi del mondo, tolemaico e copernicano)對於人類文明是一部不朽的傑作,其影響了西方科學的進步,連發現萬有引力的艾薩克·牛頓爵士(Sir Isaac Newton)都將其譽為科學史上的巨人。
西方天文數學在古希臘時代有著輝煌的成就,而其中就是人們已開始思考這個世界的模樣,在托勒密(Claudius Ptolemy)完善地心說之前,無人能解釋日月星辰流轉下有著微妙又神秘的規律,在這個時代,人們普遍地相信日月星辰是以地球為中心循著天北極而轉,因此地心體系最早被發展出來,然而這種看似理所當然的想法卻不是為所有人所抱持,因此有另一部分的人提出了非地心體系的世界觀。
地心體系
地心體系的概念是一種直覺,對於地球位處於世界的中心,這個概念在古希臘被發展開來,公元前六世紀米利都學派(Milesian school)的阿那克西曼德(Anaximander)提出了他自己的宇宙觀,這個宇宙觀最特別的地方莫過於他大膽的假設,其概念涉及今日宇宙學的最終理論,而就我們所處的世界而言,他認為地球是浮在這個宇宙之中而不需要任何支撐。形狀是兩面鼓起的圓柱體,而我們就在其中一面,而另一面則是另一個世界,這個宇宙觀被畢達哥拉斯(Pythagoras of Samos)所結合,隨後被畢達哥拉斯學派所延續,開啟了以地球為宇宙中心的理論發展,到了亞里士多德時代幾乎奠定了這樣的宇宙觀。
同心球模型
公元前四世紀,古希臘天文學家尤德瑟斯(Eudoxus of Cnidus)提出了以地球為世界中心的同心球理論,這個理論基於柏拉圖(Plato)的宇宙觀,所有天體的運行是均速的,而這個理論可以大致上分為三個部分,用作解釋一般恆星與太陽及其餘行星的運行,他主張儘管世界都以地球為中心旋轉,但其轉軸卻並不相同,以此想法來區別恆星的周日運動與太陽的南北移動,而對於行星逆行的問題則使用了複雜的多重同心球來解釋,因此最終尤德瑟斯的同心球模型除了一般恆星的同心球殼外,太陽與月球各有三個同心球殼,行星則有四個同心球殼,共計二十七個同心球殼。
進階延伸
尤德瑟斯的同心球理論看似複雜,但其原理並不難。
第一個球殼主要解釋天體的周日運動,由東向西旋轉,而由於恆星、太陽、月球及其他行星的周日運動有些許不同,因此除了背景恆星共用一個同心球殼之外,其餘天體都有自己的第一層同心球殼,也是最外層的球殼。
第二層球殼位在第一層球殼的內部,由西向東反轉,用來解釋天體的黃道周期。
第三層球殼位在第二層球殼之內,用作解釋行星的會合週期;最內層的球殼與第三層球殼則是用作解釋逆行現象。
本輪與均輪模型
公元前三世紀的阿波羅尼斯(Apollonius of Perga)使用了另一種概念來描述行星體系,這個被後來托勒密稱之為本輪與均輪的模型,其最初的概念是以本輪作為天體繞行的軌道,而每個天體各自也有獨立旋轉的軌道稱作均輪,公元前二世紀的伊巴谷(Hipparchos)也有相同的想法。
公元二世紀,托勒密在《天文學大成》(Almagest)中運用本輪與均輪的概念解釋行星逆行,以及行星遠近的亮度變化,在當時的觀測精度上算是成功的,因此很快地被人們所接受,反而同為地心體系的同心球模型卻無法解釋金星的亮度變化而遭到遺棄。
而托勒密是如何運用本輪與均輪呢?事實上,托勒密透過大量的觀測改進了阿波羅尼斯原有的想像,在托勒密的行星體系下,地球實際並不在均輪的中心,而是有些許的偏移,對於距離較近的水星與金星而言,其本輪中心位處太陽與地球的連線上;對於距離較遠的火星、木星與土星而言,它們至其本輪中心的連線恰與日地連線平行,在這些條件安排下,巧妙的解釋了行星的逆行。
圖解
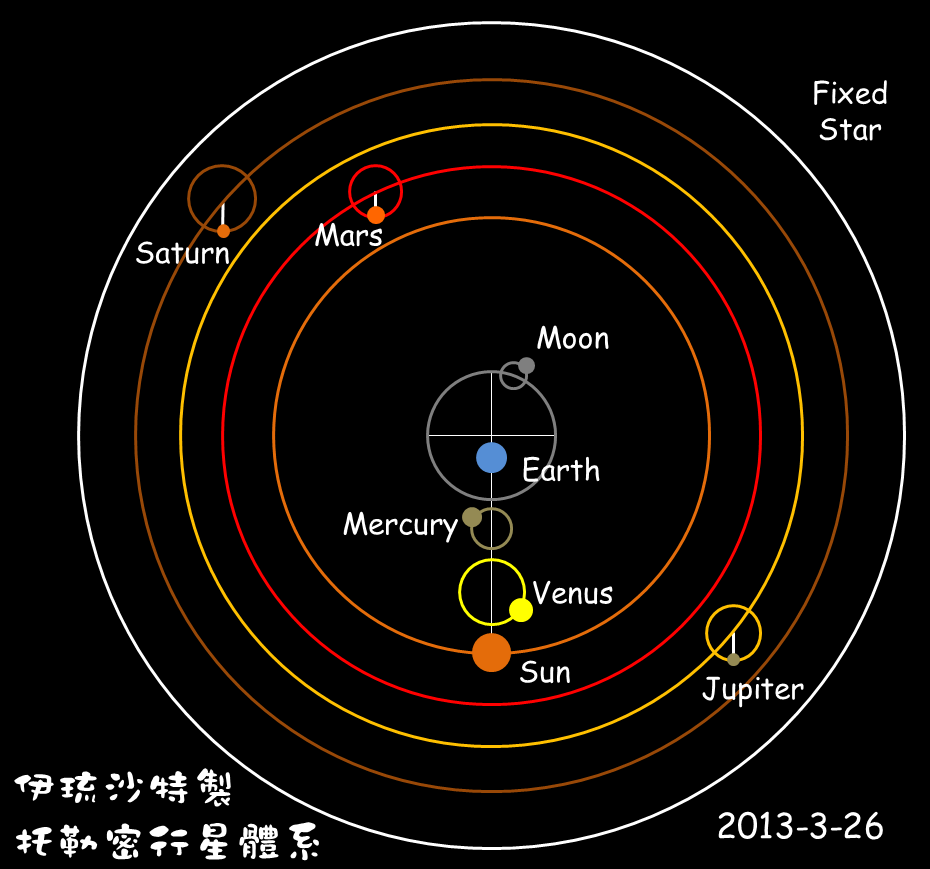
日心體系
在歷史上,提出日心體系的第一人不是哥白尼,而是古希臘天文學家亞里斯塔克(Αρίσταρχος ο Σάμιος),但是這種想法相對於同時期的亞里士多德,托勒密等人的地心主張,並未獲得充分理解與支持。
直到公元十六世紀初,近1800年後,哥白尼(Mikołaj Kopernik)才重新審視以太陽作為宇宙中心的理論,此即為日心說,隨後布魯諾(Giordano Bruno)的宣傳以及伽利略(Galileo Galilei)的觀測使得日心說開始具有說服力。
註:布魯諾因堅持日心說並極力宣揚,於公元1600年2月17日被處以火刑。
行星的和諧
這個篇名是伊琉沙有感克卜勒任務在搜尋系外行星上有卓越的貢獻,也為了紀念克卜勒(Johannes Kepler)對於近代天文學具有偉大的貢獻,因此取其著作《世界的和諧》(Harmonices Mundi)為題而名。
畢達哥拉斯的宇宙和諧
最早將和諧這種屬於美學的概念引入宇宙觀的人是畢達哥拉斯(Pythagoras of Samos),而這種概念來自他對於音律的認知加上他對於「數」的崇拜。
畢達哥拉斯最初聽到鐵匠敲打的音產生靈感進而研究,透過鐵鎚的重量找出了音程關係,發現重量比為2:1、4:3與3:2時,敲擊出來的聲音是和諧的,而後又以琴弦進行研究,發現弦長的比例也有相同的結論,這就是現代的八度音程、四度音程與五度音程。
而畢達哥拉斯認為宇宙也遵循著這個道理,以當時的宇宙觀,地球外圍是一層一層的球殼,每個行星都有各自的球殼,於是他將球殼之間的距離比搭配音程,其原則以月球作為距離地球最近的一顆星,給予一個全音程,地球與最遠的恆星恰為一個完全八度;因此地球與太陽為一個完全五度,月球與太陽則為完全四度,最後譜出了下列的天體和諧關係。
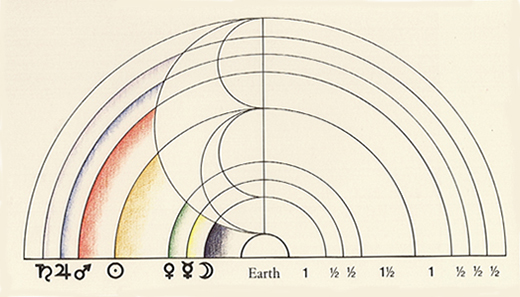
- 地球至月球為一個全音程
- 月球至水星為一個半音程
- 水星至金星為一個半音程
- 金星至太陽為小三度音程
- 太陽至火星為一個全音程
- 火星至木星為一個半音程
- 木星至土星為一個半音程
- 土星至恆星為一個半音程
註:參考資料原文為“Saturn – the fixed stars a minor third…His concept is that the Moon is the closest body and should correspond to the shortest string and Saturn is represented by the longest string of the lyre.”與前文理論有些微不同,一是對於天體和諧的安排,該文指出月球為距離地球最近星體,為最短弦,相對地,土星為最長弦,二為土星至恆星為小三度音程。
P.S. 本文原僅有提丟斯-波德定律一節,伊琉沙為充分完成這篇而再加入畢達哥拉斯與克卜勒的和諧論。
克卜勒的世界和諧
與畢達哥拉斯類似,克卜勒於公元1596年著作的《宇宙的奧秘》(Mysterium cosmographicum)中,曾試圖使用已知的五個柏拉圖立體(Platonic solid)套用在當時已知的六個行星軌道上,來完美其世界的和諧,而這個奇特的想法來自於為何太陽系恰恰只有六顆行星不多也不少?這個問題令克卜勒百思不解,直到他聯想到正多面體也恰恰只有五個,而每個正多面體都會有一個外接球與內接球,若多面體彼此環環相扣,那正好會產生六個圓形軌道,那是否就能解釋為何只有六顆行星!?
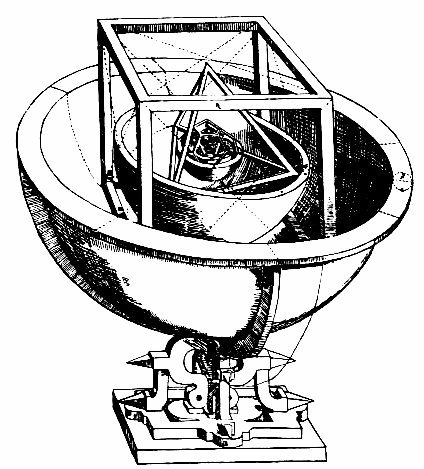
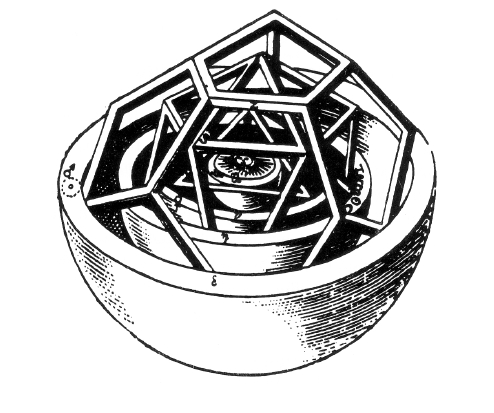
上圖是克卜勒用作解釋行星與太陽距離時說套用的模型,首先左圖可清楚看見一個正六面體(立方體)與一個正四面體,而右圖則是左圖四面體中心的放大圖,最外側是正十二面體,依序向內為正二十面體與正八面體。
- 立方體:外接圓為土星軌道,內接圓為木星軌道,所以立方體為土星與木星之間的距離。
- 正四面體:外接圓為木星軌道,內接圓為火星軌道,所以正四面體為木星與火星之間的距離。
- 正十二面體:外接圓為火星軌道,內接圓為地球軌道,所以正十二面體為火星與地球之間的距離。
- 正二十面體:外接圓為地球軌道,內接圓為金星軌道,所以正二十面體為地球與金星之間的距離。
- 正八面體:外接圓為金星軌道,內接圓為水星軌道,所以正八面體為金星與水星之間的距離。
公元十六世紀末,克卜勒(Johannes Kepler)跟隨於第谷·布拉赫(Tycho Brahe)擔任助手,在1601年第谷去世之後將大量觀測記錄都交予克卜勒,也造就了克卜勒最具影響力的著作《新天文學》(Astronomia nova)與《世界的和諧》 (Harmonices Mundi),其中著名的行星三大運動定律就出自其中。
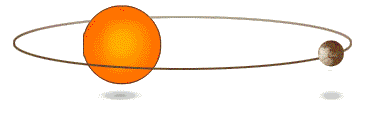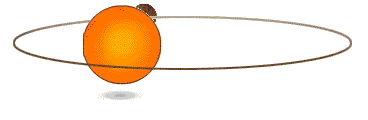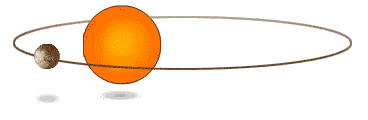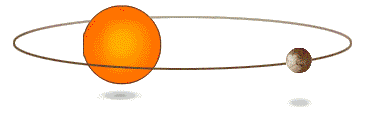
- 軌道定律:行星所運行的軌跡為一橢圓軌道。
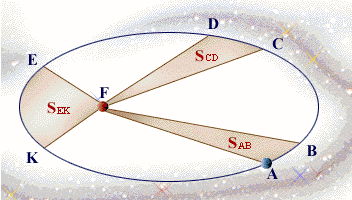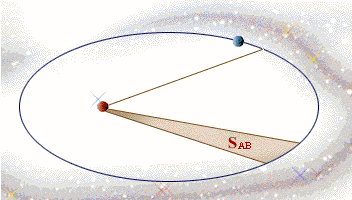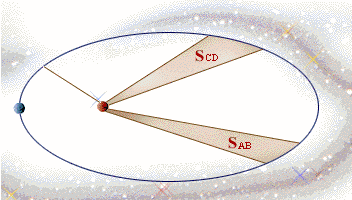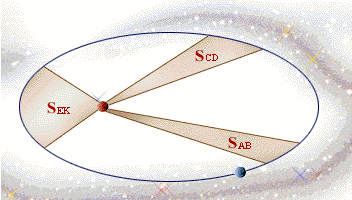
- 等面積定律:行星與太陽的連線,在單位時間內所掃過的面積相等。
- 週期定律:行星公轉週期的平方與軌道半長軸的立方成正比。
提丟斯·波德定律
提丟斯·波德定律是公元1766年由提丟斯(Johann Daniel Titius)觀察已知六顆行星的距離關係所提出的理論,後由當時的柏林天文台台長波德(Johann Elert Bode)歸納出一套公式,即波德定律,從表格中可發現行星之間隱藏著某種神秘的和諧。
| 行星 | 數列 | 導出數 | 實際距離(AU) |
| 水星 | (4+3×2-∞)/10 | 0.4 | 0.39 |
| 金星 | (4+3×20)/10 | 0.7 | 0.72 |
| 地球 | (4+3×21)/10 | 1.0 | 1.00 |
| 火星 | (4+3×22)/10 | 1.6 | 1.52 |
| →穀神星 | (4+3×23)/10 | 2.8 | 2.77 |
| 木星 | (4+3×24)/10 | 5.2 | 5.20 |
| 土星 | (4+3×25)/10 | 10 | 9.58 |
| →天王星 | (4+3×26)/10 | 19.6 | 19.23 |
| →海王星 | (4+3×27)/10 | 38.8 | 30.10 |
| →冥王星 | (4+3×28)/10 | 77.2 | 39.48 |








































